Casio ClassPad fx-CP400 Exemples Manuel d'utilisation
Page 22
Chapitre 5 : Application Graphes d’équations différentielles 22
0508
1. Lancez l’application eActivity et saisissez l’expression et la matrice
suivantes.
y
’ = exp(
x
) +
x
2
[0,1]
2. Sur le menu de l’application eActivity, tapez sur [Insert], [Strip(2)] puis sur
[DiffEqGraph].
• Un bandeau de données du graphe d’équation différentielle est inséré et la fenêtre graphique d’équation
différentielle s’affiche dans la moitié inférieure de l’écran.
3. Tirez le stylet sur «
y
’ = exp(
x
) +
x
2
» sur la fenêtre de l’application eActivity
pour sélectionner l’expression.
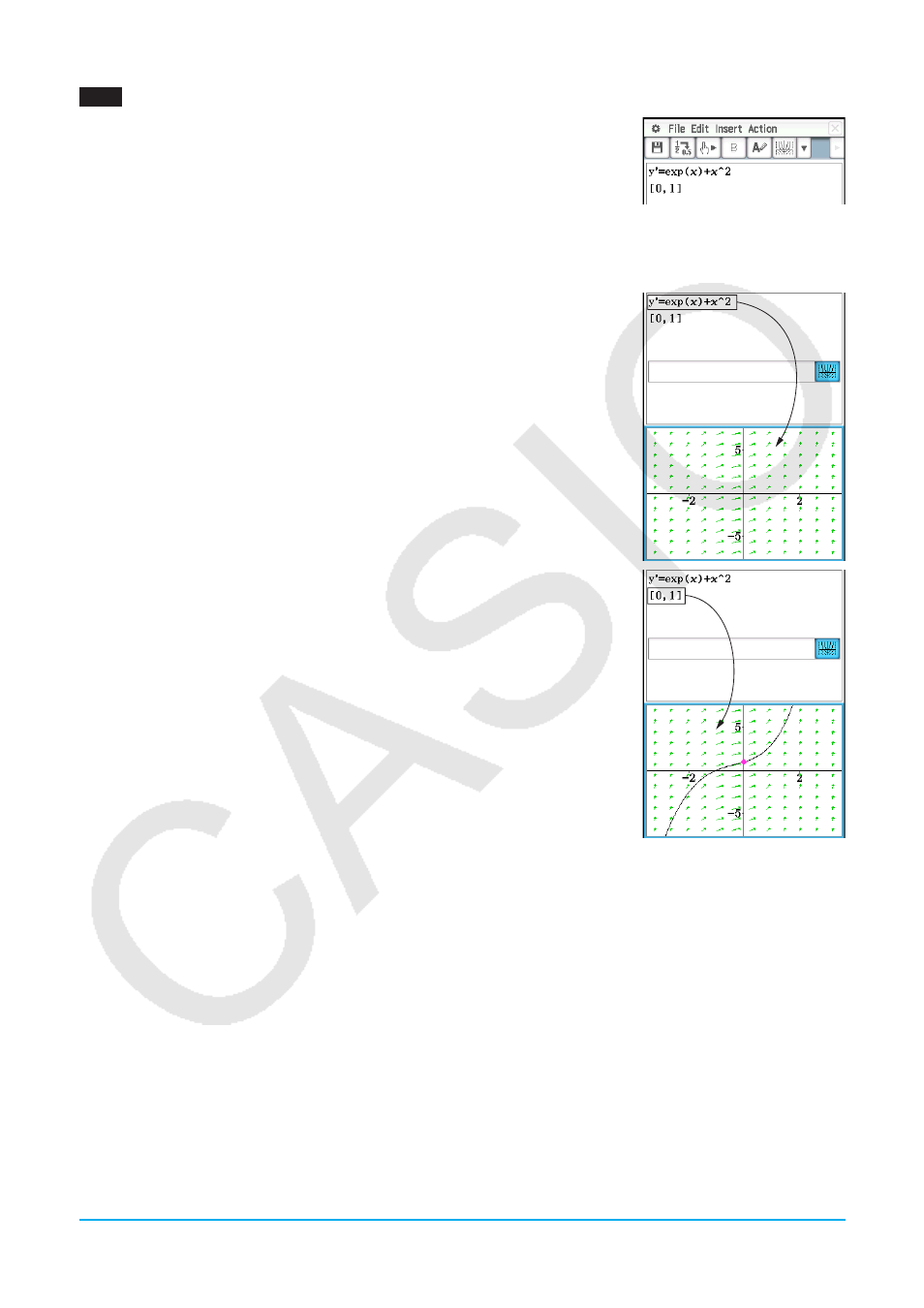
4. Déposez l’expression sélectionnée dans la fenêtre graphique d’équation
différentielle.
• Le champ de pente de
y
’ = exp(
x
) +
x
2
est tracé et l’équation enregistrée
dans l’éditeur d’équations différentielles (onglet [DiffEq]).
5. Tirez le stylet sur « [0,1] » sur la fenêtre de l’application eActivity pour
sélectionner la matrice.
6. Faites glisser la matrice sélectionnée dans la fenêtre graphique d’équation
différentielle .
• La courbe solution de
y
’ = exp(
x
) +
x
2
est tracée selon les conditions
initiales définies par la matrice et la condition initiale enregistrée dans
l’éditeur de conditions initiales (onglet [IC]).